Home
I am a quantitative research analyst at Qube Research & Technologies in Zurich. My mathematical research interests are probability theory (in particular random matrices), statistical physics, and statistical learning theory.
CV
-
BSc Mathematics
ETH Zürich
-
BSc Mathematics
LMU Munich
-
MSc Theoretical and Mathematical Physics
LMU Munich
-
MASt Mathematics
University of Cambridge
-
PhD Mathematics
IST Austria
-
Industry Sabbatical
Bosch Center for Artificial Intelligence
-
Junior Fellow
ETH Institute for Theoretical Studies
-
SNF Ambizione Fellow
ETH Zurich
-
Quantitative Research Analyst
Qube Research & Technologies
Research
My research focuses on random matrices, free probability and statistical learning theory. For a list of all publications, see the publication list, the arXiv, or my Google Scholar profile. Below are some recent or selected publications.
-
Matrix Concentration Inequalities and Free Probability II. Two-sided Bounds and Applications
Afonso Bandeira, Giorgio Cipolloni, Ramon van Handel, Dominik Schröder
preprint(2024)
We determine the approximate location of the extreme eigenvalues for a large class of random matrix models. These two-sided bounds are fundamentally beyond the reach of classical matrix concentration inequalities.
-
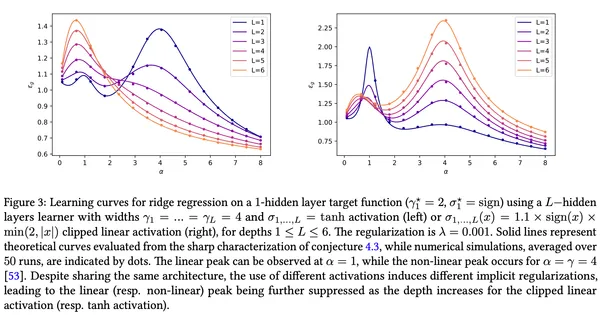
Asymptotics of Learning with Deep Structured (Random) Features
Dominik Schröder, Hugo Cui, Daniil Dmitriev, Bruno Loureiro
ICML 2024(2024)
We derive an approximative formula for the generalization error of deep neural networks with structured (random) features, confirming a widely believed conjecture. We also show that our results can capture feature maps learned by deep, finite-width neural networks trained under gradient descent.
-
Deterministic equivalent and error universality of deep random features learning
Dominik Schröder, Hugo Cui, Daniil Dmitriev, Bruno Loureiro
ICML(2023)
We show that the generalization error of deep random feature models is the same as the generalization error of Gaussian features with matched covariance, and derive an explicit expression for the generalization error.
-
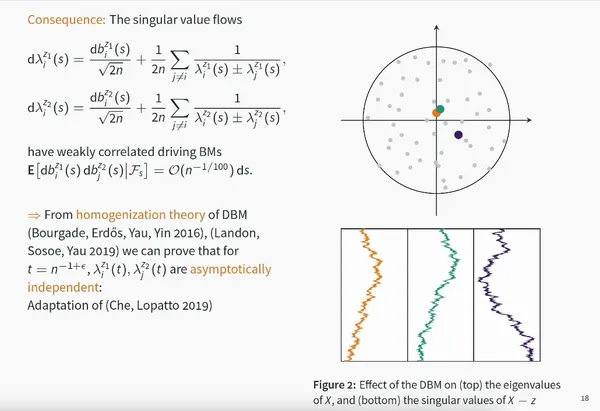
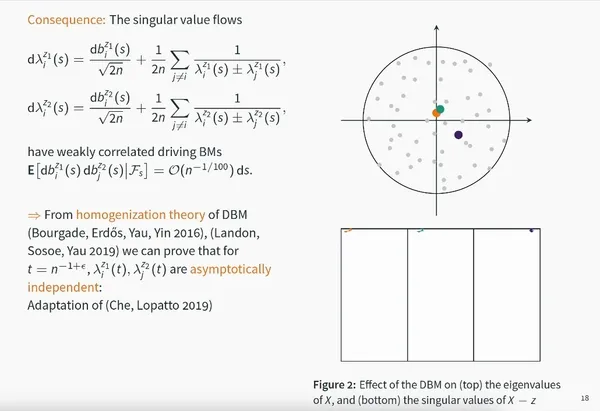
Central limit theorem for linear eigenvalue statistics of non-Hermitian random matrices
Giorgio Cipolloni, László Erdős, Dominik Schröder
Comm. Pure Appl. Math.Vol. 76 (2023)
We show that the linear statistics of random matrices with IID entries asymptotically are a rank-one perturbation of the Gaussian free field on the unit disc.
-
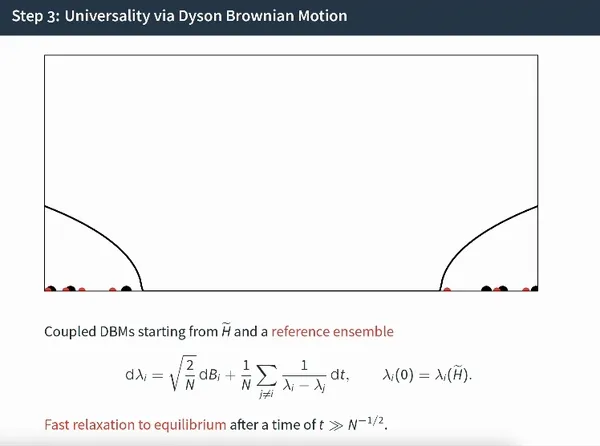
Random matrices with slow correlation decay
László Erdős, Dominik Schröder
Forum Math. SigmaVol. 7 (2017)
We prove universality for a large class of random matrices with correlated entries. This very general result has been used numerous times, also in more applied research.
-
Phase Transition in the Density of States of Quantum Spin Glasses
László Erdős, Dominik Schröder
Math. Phys. Anal. Geom.Vol. 17 (2014) | Issue 3-4
We demonstrate a transition between Gaussian and semicircular laws using q-Hermite polynomials. This work has inspired large amounts of follow-up research on the SYK model for quantum gravity.
Projects
Next to my research, I have worked on various applied machine learning and open-source software projects. Below is a list of selected projects, the full list can be found here, or on my GitHub profile.
-
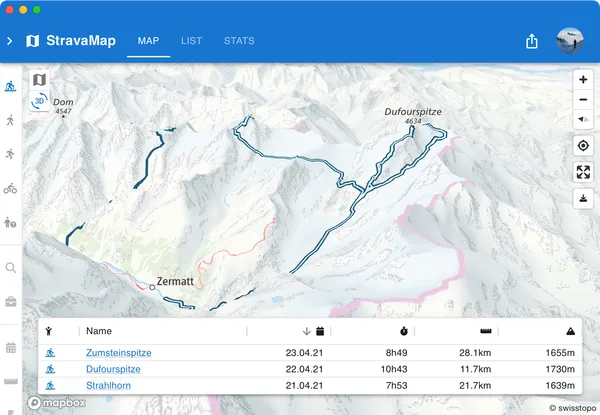
Web app to display personal outdoor activities on a map, with advanced filtering and data visualization.
-
Regression on EEG data using xResnet1d to predict the cortical silent period onset and offset. Work in progress.
Contact
- Email schroeder.dominik@gmail.com
- GitHub wirhabenzeit
- Instagram wirhabenzeit